DC Motor with PI-controller

In this example, a PI-controller is set up for speed control of a DC-motor. An equivalent circuit diagram is depicted below.

First, a continuous-time velocity controller will be used, we then change the controller to be implemented in discrete-time in Discrete-time controller. Finally, we add an outer position controller in Adding a slower outer position loop.

Modeling and simulation

The electrical part consists of a resistance and inductance. The coupling between the electrical and rotational domain is done via an electro-motive force (EMF) component. The voltage across the EMF is proportional to the angular velocity and the current is proportional to the torque. On the mechanical side, viscous friction in, e.g., a bearing and the inertia of the shaft is modelled.

A PI-controller with anti-windup measure should be used as a speed controller. A simulation is performed to verify the tracking performance of the controller and the disturbance rejection capabilities.

First, the needed packages are imported and the parameters of the model defined.

using ModelingToolkit
using ModelingToolkit: t_nounits as t
using ModelingToolkitStandardLibrary.Electrical
using ModelingToolkitStandardLibrary.Mechanical.Rotational
using ModelingToolkitStandardLibrary.Blocks
using OrdinaryDiffEq
using Plots

R = 0.5 # [Ohm] armature resistance
L = 4.5e-3 # [H] armature inductance
k = 0.5 # [N.m/A] motor constant
J = 0.02 # [kg.m²] inertia
f = 0.01 # [N.m.s/rad] friction factor
tau_L_step = -0.3 # [N.m] amplitude of the load torque step

The actual model can now be composed.

@named ground = Ground()
@named source = Voltage()
@named ref = Blocks.Step(height = 1, start_time = 0)
@named pi_controller = Blocks.LimPI(k = 1.1, T = 0.035, u_max = 10, Ta = 0.035)
@named feedback = Blocks.Feedback()
@named R1 = Resistor(R = R)
@named L1 = Inductor(L = L)
@named emf = EMF(k = k)
@named fixed = Fixed()
@named load = Torque()
@named load_step = Blocks.Step(height = tau_L_step, start_time = 1.3)
@named inertia = Inertia(J = J)
@named friction = Damper(d = f)
@named speed_sensor = SpeedSensor()

connections = [connect(fixed.flange, emf.support, friction.flange_b)
               connect(emf.flange, friction.flange_a, inertia.flange_a)
               connect(inertia.flange_b, load.flange)
               connect(inertia.flange_b, speed_sensor.flange)
               connect(load_step.output, load.tau)
               connect(ref.output, feedback.input1)
               connect(speed_sensor.w, feedback.input2)
               connect(feedback.output, pi_controller.err_input)
               connect(pi_controller.ctr_output, source.V)
               connect(source.p, R1.p)
               connect(R1.n, L1.p)
               connect(L1.n, emf.p)
               connect(emf.n, source.n, ground.g)]

@named model = ODESystem(connections, t,
    systems = [
        ground,
        ref,
        pi_controller,
        feedback,
        source,
        R1,
        L1,
        emf,
        fixed,
        load,
        load_step,
        inertia,
        friction,
        speed_sensor
    ])
model = complete(model)

Now the model can be simulated. Typical rotational mechanical systems are described via DAE (differential algebraic equations), however in this case, ModelingToolkit can simplify the model enough so that it can be represented as a system of ODEs (ordinary differential equations).

sys = structural_simplify(model)
prob = ODEProblem(sys, unknowns(sys) .=> 0.0, (0, 2.0))
sol = solve(prob, Tsit5())

p1 = Plots.plot(sol.t, sol[inertia.w], ylabel = "Angular Vel. in rad/s",
    label = "Measurement", title = "DC Motor with Speed Controller")
Plots.plot!(sol.t, sol[ref.output.u], label = "Reference")
p2 = Plots.plot(sol.t, sol[load.tau.u], ylabel = "Disturbance in Nm", label = "")
Plots.plot(p1, p2, layout = (2, 1))

Discrete-time controller

Until now, we have modeled both the physical part of the system, the DC motor, and the control systems, in continuous time. In practice, it is common to implement control systems on a computer operating at a fixed sample rate, i.e, in discrete time. A system containing both continuous-time parts and discrete-time parts is often referred to as a "sampled-data system", and the ModelingToolkit standard library together with ModelingToolkitSampledData.jl contain several components to model such systems.

Below, we re-model the system, this time with a discrete-time controller: DiscretePIDStandard. To interface between the continuous and discrete parts of the model, we make use of a Sampler and ZeroOrderHold blocks. Apart from the three aforementioned components, the model is the same as before.

using ModelingToolkitSampledData
using JuliaSimCompiler

z = ShiftIndex()
@mtkmodel DiscreteClosedLoop begin
    @structural_parameters begin
        use_ref = true
    end
    @components begin
        ground = Ground()
        source = Voltage()
        ref = Blocks.Step(height = 1, start_time = 0, smooth = false)
        sampler = Sampler(dt = 0.005)
        pi_controller = DiscretePIDStandard(
            K = 1, Ti = 0.035, u_max = 10, with_D = false)
        zoh = ZeroOrderHold()
        R1 = Resistor(R = R)
        L1 = Inductor(L = L)
        emf = EMF(k = k)
        fixed = Fixed()
        load = Torque()
        load_step = Blocks.Step(height = tau_L_step, start_time = 1.3)
        inertia = Inertia(J = J)
        friction = Damper(d = f)
        speed_sensor = SpeedSensor()
        angle_sensor = AngleSensor()
    end

    @equations begin
        connect(fixed.flange, emf.support, friction.flange_b)
        connect(emf.flange, friction.flange_a, inertia.flange_a)
        connect(inertia.flange_b, load.flange)
        connect(inertia.flange_b, speed_sensor.flange, angle_sensor.flange)
        connect(load_step.output, load.tau)
        if use_ref
            connect(ref.output, pi_controller.reference)
        end
        connect(speed_sensor.w, sampler.input)
        connect(sampler.output, pi_controller.measurement)
        connect(pi_controller.ctr_output, zoh.input)
        connect(zoh.output, source.V)
        connect(source.p, R1.p)
        connect(R1.n, L1.p)
        connect(L1.n, emf.p)
        connect(emf.n, source.n, ground.g)
    end
end

@named disc_model = DiscreteClosedLoop()
disc_model = complete(disc_model)
ssys = structural_simplify(IRSystem(disc_model)) # Conversion to an IRSystem from JuliaSimCompiler is required for sampled-data systems

disc_prob = ODEProblem(ssys, [unknowns(disc_model) .=> 0.0; disc_model.pi_controller.I(z-1) => 0; disc_model.pi_controller.eI(z-1) => 0], (0, 2.0))
disc_sol = solve(disc_prob, Tsit5())

Plots.plot(sol.t, sol[inertia.w], ylabel = "Angular Vel. in rad/s",
    label = "Measurement (cont. controller)", title = "DC Motor with Speed Controller")
Plots.plot!(disc_sol.t, disc_sol[inertia.w], ylabel = "Angular Vel. in rad/s",
    label = "Measurement (disc. controller)", title = "DC Motor with Discrete-time Speed Controller", legend=:bottomleft, dpi=600)
lens!([1.2, 1.6], [0.75, 1.02], inset=(1, bbox(.6, .5, .3, .4))) # 1 is subplot index

In the plot above, we compare the result of the discrete-time control system to the continuous-time result from before. We see that with the chosen sample-interval of dt=0.005 (provided to the Sampler block), we have a slight degradation in the control performance as a consequence of the discretization.

Adding a slower outer position loop

Below, we add an outer control loop that controls the position of the motor by manipulating the reference to the inner speed controller. This is a common control strategy, often referred to as cascade control.

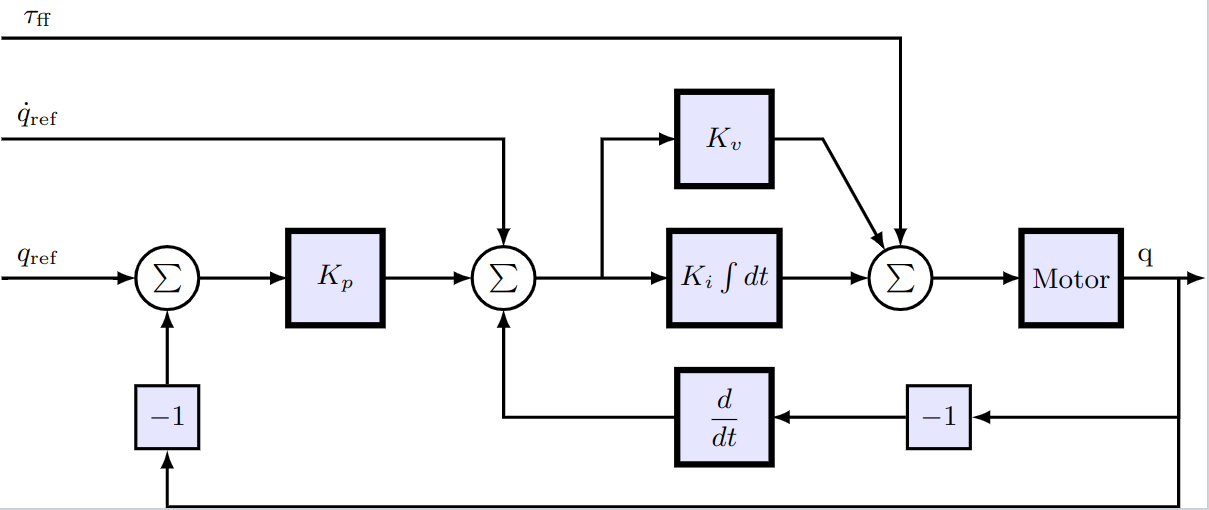
@mtkmodel Cascade begin
    @components begin
        inner = DiscreteClosedLoop(use_ref = false)
        sampler = Sampler(clock = Clock(0.005))
        # cc = ClockChanger(from = get_clock(sampler), to = get_clock(inner.sampler)) # Currently deactivated due to bug
        cc = Gain(k = 1)
        ref = Blocks.Ramp(height = 1, start_time = 0.05, duration = 0.85, smooth = false)
        ref_diff = DiscreteDerivative() # This will differentiate q_ref to q̇_ref
        add = Blocks.Add()      # The middle ∑ block in the diagram
        p_controller = DiscretePIDStandard(K = 20, with_D = false, with_I = false)
    end
    @parameters begin
        O = 0
    end
    begin
        from = get_clock(sampler)
        to = get_clock(inner.sampler)
    end
    @equations begin
        # cc.y(ShiftIndex(to)) ~ ClockChange(; from, to)(cc.u(ShiftIndex(from))) + O
        # cc.y ~ ClockChange(; from, to)(cc.u) + eps()^10
        # cc.y ~ cc.u
        connect(ref.output, p_controller.reference, ref_diff.input)
        connect(ref_diff.output, add.input1)
        connect(add.output, cc.input)
        connect(cc.output, inner.pi_controller.reference)
        connect(p_controller.ctr_output, add.input2)
        connect(inner.angle_sensor.phi, sampler.input)
        connect(sampler.output, p_controller.measurement)
    end
end

@named cascade = Cascade()
cascade = complete(cascade)
ssys = structural_simplify(IRSystem(cascade))
i = cascade.inner
cascade_prob = ODEProblem(ssys, [
    unknowns(cascade) .=> 0.0;
    i.pi_controller.I(z-1) => 0;
    i.pi_controller.eI(z-1) => 0;
    cascade.p_controller.I(z-1) => 0;
    cascade.ref_diff.u(z-1) => 0.0;
    cascade.cc.u(z-1) => 0.0;
    ], (0, 2))
cascade_sol = solve(cascade_prob, Tsit5())
Plots.plot(cascade_sol, idxs = [i.inertia.phi, i.inertia.w, i.zoh.u])